VECTOR &CALCLUS

Vectors - Introduction

Vector quantities

Physical quantities that need both magnitude and direction to completely define them are called Vector quantities.

Scalar quantities

Physical quantities that need only magnitude to completely define them are called Scalar quantities.

Representation of Vectors

• Analytical representation
  a→, A→, b→, B→, etc.. They are the variables with an arrow drawn on top.

Note

1. No matter what the direction of a specific vector is, the arrow is always drawn from left to right on the top of variable name as shown above.

2. In some books, vectors are also represented simply by a bold alphabet (without any arrow on top). E.g. a, A, b, B, etc. They have the same meaning as a→, A→, b→, B→, etc. respectively.

• Pictorial/Diagrammatic representation
  Vectors are shown pictorially by an arrow. Length of the arrow indicates the “magnitude” and direction in which the arrow head is pointing indicates the “direction”.

Magnitude of a vector X→ is indicated by |X|→ or simply X.

Negative of a Vector

Negative of a vector simply reverses the direction of the vector. Magnitude stays unaffected.

Multiplication of a vector by scalar

The magnitude of the vector is multiplied by the scalar. Direction remains unaffected.

Vectors - Terminologies and General Properties

Representation of Vectors

• Analytical representation
  a→, A→, b→, B→, etc.. They are the variables with an arrow drawn on top.

Note

1. No matter what the direction of a specific vector is, the arrow is always drawn from left to right on the top of variable name as shown above.

2. In some books, vectors are also represented simply by a bold alphabet (without any arrow on top). E.g. a, A, b, B, etc. They have the same meaning as a→, A→, b→, B→, etc. respectively.

• Pictorial/Diagrammatic representation
  Vectors are shown pictorially by an arrow. Length of the arrow indicates the “magnitude” and direction in which the arrow head is pointing indicates the “direction”.

Magnitude of a vector X→ is indicated by |X|→ or simply X.

Parallel Vectors

• Vectors are regarded as parallel if they point in the same direction.
• The angle between the vectors is 0 degrees.
• The vectors may or may not have their magnitudes equal.

Anti-parallel Vectors

• Vectors are regarded as anti-parallel if they point in exactly opposite directions.
• The angle between the vectors is 180 degrees.
• The vectors may or may not have their magnitudes equal.

Equality of Vectors

Two vectors are regarded as equal if and only if,

• Their magnitudes are same, and
• Their directions are same.

Negative of a Vector

Negative of a vector simply reverses the direction of the vector. Magnitude stays unaffected.

Multiplication of a vector by scalar

The magnitude of the vector is multiplied by the scalar. Direction remains unaffected.

Unit Vector

• Unit vectors have magnitude = 1.
• They are special vectors that represent specific directions.
• A vector of any size could be created in that specific direction (represented by unit vector) by simply multiplying a scalar with the unit vector.
• They are distinguished from standard vector variables by having a x̂ (cap) symbol instead of x→(vector) symbol.

• Because any vector can be created in the direction of unit vector by simple multiplication of a scalar number, interpret X→ as,
  • X→ = |X|→ X̂
  • Scalar number |X|→, which represents the magnitude, is multiplied to X̂, which represents the direction, to create X→.
  Hence, X̂ = X→|X|→

Zero Vector

• Zero Vector is a Mathematical concept and has little significance in Physics.
• Zero Vector has magnitude = 0.
• Zero vector has indeterminate direction.
• It is represented by 0→
• It is defined mathematically to handle cases like: a→ - a→ = 0
• 
  

  
  

  Vectors - Triangle Law of Addition

Triangle Law of Addition (Two vectors)

Draw the vectors in pictorial form.

Choose any of the two vectors as the first and place the second vector’s tail on the head of the first.

Draw a third vector joining the tail of the first to the head of the second. This vector is called the “resultant” which represents the sum of the two vectors. The red and blue line below represent the resultant in each case.

It can be noted that the vector sum obtained by taking either vector is exactly the same (Red and Blue vectors are identical in both magnitude and direction)

Triangle Law of Vector Addition (Multiple Vectors)

Draw all the vectors in pictorial form. (Three considered here)

Choose any two of them and add them according to the triangle law. (a→ and b→ chosen here)

Now add the resultant of the sum to the next vector (third vector in this case).

The resultant obtained at the end, the F→, is the vector sum of the three vectors considered.

In case of more than three vectors, Point 2 and Point 3 could be repeated till the final resultant is obtained.

Triangle Law of Vector addition (Multiple Vectors) – Direct Method

Consider the same set of three vectors taken in the last case.

Choose any one of them as the first vector. Now place the second vector’s tail on the head of the first. Also, place the third vector’s tail on the head of second simultaneously.

If there are more vectors to be added, they can be stacked up in the way.

Now draw the resultant vector, F→, from the tail of the first to the head of the last vector. (last vector is the third one in this case)

Polygon Law (Extended version of Triangle Law)

Consider four vectors x→, y→, z→, w→

Place them in “tail to head” fashion, which is, the tail of a vector should be placed on the head of the previous vector.

Complete the polygon by joining the tail of the first vector to the head of the last vector.

The vector obtained is the Resultant. Tail of the resultant coincides with the tail whereas, the head of the resultant coincides with the head of the last vector.

Vectors - Parallelogram Law of Addition

Parallelogram Law of Addition (Two Vectors)

Draw the vectors in pictorial form.

Place the vectors such that their tails coincide.

Complete a parallelogram by drawing lines parallel to each of the vectors.

The diagonal passing through the point of contact of the tails is the resultant vector.

Here, S→ is the final resultant obtained from the parallelogram law of addition.

Parallelogram Law of Addition (Multiple Vectors)

Draw all the vectors in pictorial form. (Three considered here).

Choose any two of them and add them according to the parallelogram law. (a→ and b→chosen here)

Now add the resultant of the sum to the next vector (third vector in this case).

The resultant obtained at the end, the F→, is the vector sum of the three vectors considered.

In case of more than three vectors, Point 2 and Point 3 could be repeated till the final resultant is obtained.

Note

1. Triangle Law and Parallelogram Law yield the same resultant.

2. Each method is suited for different situations, more of which you will learn in future chapters.

3. But, at any time, both are equally valid methods to find the sum of two vectors

Vectors - Derivation of Addition Formula

Formula to find the magnitude and direction of the resultant vector

Note

• Parallelogram law of addition is used for this derivation.
• Triangle Law method will yield the same result.

Derivation

a→ and b→ are considered as the original vectors. Angle between them is ‘θ’

S→ is the resultant vector.

Aim is to find the magnitude (length) of the resultant vector (|S|→) and the angle ‘α’ (angle between the resultant and a→).

Construction −

• Extend the line AD
• Drop a perpendicular from point C on to the extended line. Perpendicular meets the line at point B.

▱ AEDC is a parallelogram, hence AE = DC. Hence, DC = |b|→ or DC = b.

▱ AEDC is a parallelogram, hence AE∥DC. Also, AD is a transversal to it. This implies ∠EAD = ∠CDB = θ.

Now, in △BCD,

• sin θ = BCDC, hence, BC = |b|→ sin θ or b sin θ
• cos θ = BDCD, hence, BD = |b|→ cos θ or b cos θ

Finally, in △ABC,

• Using Pythagoras’ theorem, |S|→² = (|a|→+ |b|→ cos θ)² + (|b|→ sin θ)²
• This implies, |S|→ = √(|a|→ + |b|→ cos θ)²+ (|b|→ sin θ)²

This implies, |S|→ = √|a|→² + |b|→² + 2(|a|→)(|b|→)cos θ .. PROVED

Also, tan θ = |b|→sin θ|a|→ + |b|→cos θ... PROVED

Note

1. The magnitude of resultant depends on two factors −

• The magnitudes of original vectors
• Angle between the original vectors

2. The sign convention for the angle is −

• Anticlockwise direction is positive (+)
• Clockwise direction is negative (-)

Vectors - Subtraction

Concept in Subtraction of Vectors

• Let’s say vector b→ has to be subtracted froma→.
• The resultant vector, D→ = a→ - b→
• This should be interpreted as D→ = a→ + (−b→)
• Now, −b→ is simply b→ in reversed direction.
• So, D→ is simply the addition of a→ with the “reversed b→”.

Subtraction using Triangle Law

Consider vectors a→ and b→.

In order to subtract b→, it must be reversed.

Carry out the operation D→ = a→ + (−b→)

D→ here is the resultant of subtraction.

Subtraction using Parallelogram Law

Consider vectors a→ and b→

In order to subtract a→, it must be reversed.

Carry out the operation D→ = a→ + (−b→)

D→ here is the resultant of subtraction.

Vectors - Derivation of Subtraction Formula

Magnitude of the resultant vector (Formula)

For subtraction, S→ = a→ − b→, replace ′θ′ with ‘(π − θ)′

D = √a² + b² + 2abcos(π - θ)

This implies, D = √a² + b² + 2abcos(π - θ)[because cos(π − θ) = − cos(θ)]

Direction of the Resultant Vector (Formula)

For subtraction, S→ = a→ − b→, replace ′θ′ with ‘(π − θ)′

tan α = b sin(π - θ)a + b cos(π - θ)

This implies, tan α = b sin θa - b cos θ [because cos(π − θ) = − cos(θ)]

[IMPORTANT NOTE: Sign Convention must be taken carefully]

Vectors - Resolution

Concept of Resolution

The concept of resolution could be understood in contrast to the concept of addition.

Let’s say a→ and b→ are added to get S→. This is the process of addition.

Now, S→ is broken to obtain a→ and b→ back. This is the process of resolution.

A vector can be resolved into many different vectors. Understand this with following example −

• Let’s say two numbers 4 and 6, are added to obtain 10; 4 + 6 = 10
• Now 10 is broken or resolved, and the numbers added are obtained back; 10 = 4 + 6
• But, 10 can also be resolved into many other numbers like;
  10 = 5 + 5;
  10 = 3 + 7;
  10 = 2 + 8;
  10 = 1 + 9;
  10 = 2 + 5 + 3;
  10 = 1 + 2 + 3 +4; etc
• In the same fashion, one can understand that a vector can essentially be resolved (broken) to obtain multiple vectors of different magnitudes and directions.

In Physics, vectors would be mainly resolved only along the coordinate axes, X, Y and Z.

Resolving a vector along X and Y axis

Draw the vector to be resolved on an X-Y plane.

Label and create the constructions on figure as shown below.

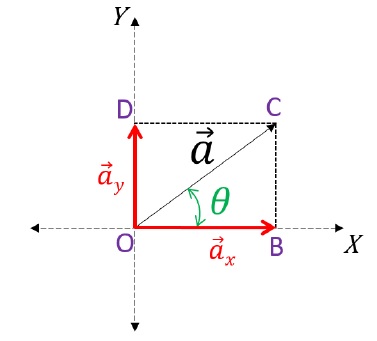
One can see that the setup appears to be of the Parallelogram law of vector addition. Here, two vectors a→_x and a→_y appear to be added to obtain a→.

Therefore, we can say that a→_x and a→_y are the resolved output of a→. (Because a→ has been broken back to its components)

a→_x is the x-component and a→_y is the y-component of a→.

To find the magnitudes of each component,

In △OBC:

cos θ = OBOC; Therefore, OB = OC cos θ

Therefore, |a_x|→ = |a|→ cos θ [Magnitude of x-component]

sin θ = BCOC; Therefore, BC = OC sin θ; Also, BC = OD(Opposite sides of Rectangle);

Therefore, |a_y|→ = |a|→ sin θ [Magnitude of y-component]

Note

General Rule of Thumb −

The subtended angle will always touch one of the components. Whichever component the given angle touches or the given angle is subtended with, that will be the cos component of the given vector. The other is automatically the sin component.

Unit Vectors along co-ordinate axes

There are special unit vectors designated by convention for the co-ordinate axes.

î, ĵ, and k̂, respectively represent X, Y, and Z axes.

By property of unit vectors, |î| = |ĵ| = |k̂| = 1

Writing Vectors in component form (Using coordinate axes unit vectors)

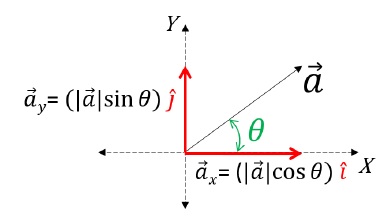
We know that a vector can be expressed as a product of its magnitude and direction. Therefore,

• a_x→ = |a_x|→ î;
  Magnitude of a_x→, which is |a_x|→, is multiplied to the direction in which a_x→lies, which is the direction of x-axis, represented by the unit vector î.
• a_y→ = (|a_y|→ sin θ) ĵ;
  Magnitude of a_y→, which is |a_y|→, is multiplied to the direction in which a_y→lies, which is the direction of y-axis, represented by the unit vector ĵ.
• Now we know that, a→ = a_x→ + a_y→;
Therefore, a→ = (|a|→ cos θ) î + (|a|→ sin θ) ĵ [Final Component Form]

Addition and Subtraction of Vectors in component form (Expressed as unit vectors)

Consider the following figure −

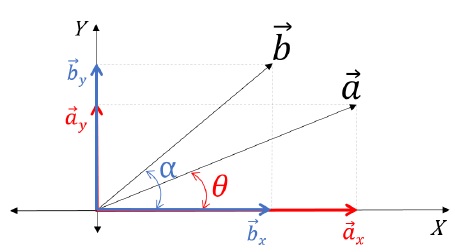
Expressing a→ in component form,

• a→ = a_x→ + a_y→;
• a→ = |a_x|→ î + |a_y|→ ĵ;
• a→ = |a|→ cos θ î + |a|→ sin θ ĵ

Expressing b→ in component form,

• b→ = b_x + b_y→;
• b→ = |b_x|→ î + |b_y|→ ĵ
• b→ = |b|cos α î + |b|→ sin α ĵ

Operation, S→ = a→ + b→;

• S→ = a→ + b→ = (|a_x|→ î + |a_y|→ ĵ) + (|b_x|→ î + |b_y|→ ĵ);
• This implies, S→ = (|a_x|→ + |b_x|→) î + (|a_y|→ + |b_y|→) ĵ;
• Hence, S→ = (|a|→ cos θ + |b|→ cos α) î + (|a|→ sin θ + |b|→ sin α)ĵ [Final Sum]

Operation, S→ = a→ − b→;

• S→ = a→ + b→ = (|a_x|→ î - |a_y|→ ĵ) + (|b_x|→ î - |b_y|→ĵ);
• This implies, S→ = (|a_x|→ - |b_x|→) î + (|a_y|→ - |b_y|→) ĵ;
• Hence, S→ = (|a|→ cos θ - |b|→ cos α) î + (|a|→ sin θ - |b|→ sin α)ĵ [Final Difference]

Vectors - Dot Product

The Concept

There are only three ways in which Physical Quantities could be multiplied to each other −

Scalar multiplied to a Scalar

Because both the quantities carry just the magnitude, they can be multiplied by the rules of standard multiplication.

Scalar multiplied to a Vector

• We have studied this in the previous video of Terminologies and Basic Properties.
• The magnitude of the vector gets multiplied to the scalar.
• Direction remains unaffected.

Vector multiplied to a Vector

• Two products are defined for multiplication of a vector with another vector.
• Dot Product which is also called Scalar Product
• Cross Product which is also called Vector Product

In this topic we will discuss Dot product in detail.

Dot Product

Dot product between two vectors is defined as −

a→.b→ = ab cos θ

It can also be written as −

a→.b→ = |a|→|b|→ cos θ [We know that |a|→ or a, both represent the magnitude of a→]

Method to find the dot product

Consider the two vectors, a→ and b→.

Place them in a way such that their tails coincide, just like we do while using Parallelogram Law.

Take the value of ‘θ’ by the right sign convention.

Carry on the dot product operation.

a→.b→ = abcos θ

Important Observations

Result of the dot product is a scalar quantity. For the same reason, there is no resultant in case of the scalar product (The result is not a vector).

If the angle θ = 0^o or 0 radians,

• Vectors are parallel to each other.
• the value of cos0 = 1.
• This is the maximum value ‘cosθ’ function can take.
• The dot product is maximum when the angle between them is 0^o or 0 rad. The value is, a→.b→ = ab

If the angle θ = 90^o or θ = π2 radians,

Vectors are perpendicular to each other.

cos π2 = 0

The value of dot product is 0 (zero), a→.b→ = 0

Properties of Dot Product

Dot product is Commutative −

• a→.b→ = b→.a→(each equal to abcos θ)
• Dot product is Distributive
• a→.(b→ + c→) = a→.b→ + a→.c→

Associative property is not applicable to dot product.

Same rules can be used on coordinate axis unit vectors, î, ĵ and k̂.

î.î = ĵ.ĵ = k̂. k̂= 1

• When a unit vector is multiplied to itself in dot product fashion, the result is always 1.
• î.î = |î| |î|cos0 = 1×1×1 = 1
  • Magnitude of any unit vector is always 1. Hence, |î| = 1.
  • Both are the same unit vectors hence they are parallel to each other. Hence, θ = 0 radians.

î.ĵ = ĵ.k̂ = k̂.î = 0

• When one of these unit vectors (î, ĵ or k̂) is multiplied to the other, the result is always 0.
  • For example, î.ĵ = |î||ĵ|cos π2 = 1×1×0 = 0
  • Magnitude of any unit vector is always 1. Hence, |î| = 1.
  • î, ĵ and k̂ are mutually perpendicular to each other. Hence, θ = π2 radians.

Also, because dot product is commutative, ĵ.î = k̂.ĵ = î.k̂ = 0

Dot Product involving two vectors

Here, a→ = (a_x î + a_y ĵ + a_z k̂)

Also,b→ = (b_x î + b_y ĵ + b_z k̂)

Therefore, S→ = a→.b→ implies,

• P = (a_x î + a_y ĵ + a_z k̂) . (b_x î + b_y ĵ +b_z k̂)
• P = (a_xb_x) î.î + (a_yb_y) î.ĵ + (a_xb_z) î.k̂ + (a_yb_x) ĵ.î + (a_yb_y) ĵ.ĵ + (a_yb_z) ĵ.k̂ + (a_zb_x) k̂.î + (a_zb_y) k̂.ĵ + (a_zb_z) k̂.k̂
• We know that î.î = ĵ.ĵ = k̂.k̂ = 1 and every other combination of î, ĵ and k̂ gives a 0(zero) answer.
• Hence, P = a_xb_x + a_yb_y + a_zb_z

Vectors - Cross Product

The Concept

There are only three ways in which Physical Quantities could be multiplied to each other −

Scalar multiplied to a Scalar

Because both the quantities carry just the magnitude, they can be multiplied by the rules of standard multiplication.

Scalar multiplied to a Vector

• We have studied this in the previous video of Terminologies and Basic Properties.
• The magnitude of the vector gets multiplied to the scalar.
• Direction remains unaffected.

Vector multiplied to a Vector

• Two products are defined for multiplication of a vector with another vector.
• Dot Product which is also called Scalar Product
• Cross Product which is also called Vector Product

In this topic, we will discuss Cross product in detail.

Cross Product

Cross product between two vectors is defined as −

a→ x b→ = ab sin θ n̂

It can also be written as −

a→×b→ = |a|→|b|→ sin θ n̂ [We know that |a|→ or a, both represent the magnitude of a→]

Method to find the dot product

Consider the two vectors, a→ and b→.

Place them in a way such that their tails coincide, just like we do while using Parallelogram Law.

To calculate the magnitude of the resultant P→ = a→×b→, use the equation of cross product −

• |P|→ = |a→xb→| = ab sin θ

To calculate the direction of resultant, one needs to understand Right Hand Thumb Rule.

• Right Hand Thumb Rule
• Right hand should be placed on top of the first vector (in this case, a→ because that is written first) such that the palm faces the second vector.
• All fingers should be curled (except the Thumb) towards the second vector.
• The direction in which the thumb points gives the direction of n̂ or P→

Applying Right Hand Thumb Rule in this case −

The resultant vector, a→xb→, is perpendicular to both a→ and b→ individually.

Same idea can be expressed by the following equation: a→.n̂ = b→.n̂ = 0 [because the angle between them is 90^o]

Important Points

The direction of the resultant vector is perpendicular to both the original vectors multiplied.

If the angle θ = 0^o or 0 radians,

• Vectors are parallel to each other.
• the value of sin0 = 0.
• he magnitude of cross product is 0 (zero), a→×b→ = 0

If the angle θ = 90^o or θ = π2 radians,

• Vectors are perpendicular to each other.
• sin π2 = 1
• This is the maximum value ‘sin θ’ function can take.
• The magnitude of cross product is maximum when the angle between them is 90^o or π2 radians.
• |a→xb→| = ab

Properties of Cross Product

Cross product is NOT Commutative

• a→xb→ ≠ b→xa→, [due to right hand thumb rule]
• Rather, a→xb→ = −(b→xa→)

• Red vector indicates a→xb→ (red angle θ indicates the correct direction by Right Hand Thumb Rule) while, green vector indicates b→xa→ (green angle θ indicates the correct direction by Right Hand Thumb Rule). It can be clearly seen that a→xb→ = -(b→xa→).

Cross product is Distributive −

• a→x(b→ + c→) = a→xb→ + a→xc→

Cross product is NOT Associative −

• a→x(b→xc→) ≠ (a→xb→)xc→

Cross product on standard unit vectors

• î x î = ĵ x ĵ = k̂ x k̂ = 0 [Vectors are parallel]
• î x ĵ = k̂; ĵ x k̂ = î; k̂ x î = ĵ [Right hand thumb rule]
• ĵ x î = -k̂; k̂ x ĵ = -î; î x k̂ = -ĵ [Right hand thumb rule]

These results can be observed by applying Right Hand Thumb Rule on coordinate axes.

To memorize these results, following diagram can be used −

Above diagram is simple to remember.

• î, ĵ and k̂ are drawn respectively in clockwise direction.
• They are connected by clockwise turning arrows.

Whenever any two standard unit vectors are crossed, they always yield the third one as the result.

Only the sign of the resultant changes based on which is the first vector.

• E.g. î x ĵ = k̂ while, ĵx î = -k̂

Therefore, in the diagram, look for the position of second vector with respect to the first.

• If its placed clockwise, the resultant will have positive sign.

Illustration −

• ĵ x k̂ = + î [k̂ is situated clockwise to ĵ. Hence, the result is positive î]
• î x k̂ = − ĵ [k̂ is situated anti-clockwise to î. Hence, the result is negative ĵ]

Cross Product involving two vectors in component form – Standard Method

Here, a→ = (a_x î + a_y ĵ + a_z k̂)

Also, b→ = (b_x î + b_y ĵ + b_z k̂)

Therefore, S→ = a→ x b→, implies,

• P = (a_x î + a_y ĵ + a_z k̂) x (b_x î + b_y ĵ + b_z k̂)
• P = (a_xb_x) î x î + (a_xb_y) î x ĵ + (a_xb_z) î x k̂ + (a_yb_x) ĵ x î + (a_yb_y) ĵ x ĵ + (a_yb_z) ĵ x k̂ + (a_zb_x) k̂ x î + (a_zb_y) k̂ x ĵ + (a_zb_z) k̂ x k̂
• Using the diagram below,
  
  î x î = 0; î x ĵ = + k̂; î x k̂ = - ĵ; ĵ x î = - k̂; ĵ x ĵ = 0; ĵ x k̂ = î; k̂ x î = ĵ; k̂ x ĵ = - î; k̂ x k̂ = 0
• P→ = (a_xb_y) k̂ + (a_xb_z) (- ĵ) + (a_yb_x) (- k̂) + (a_yb_z) î + (a_zb_x) ĵ + (a_zb_y) (- î)
• P→ = (a_yb_z - a_zb_y) î + (a_zb_x - a_xb_z) ĵ + (a_xb_y - a_yb_x) k̂

Cross Product involving two vectors in component form – Determinant Method

• As a student, you will study about determinants in detail in Mathematics.
• For now, let’s try and understand basic approach of solving a determinant and its usefulness in calculating cross product with speed.
• Let’s say, a→ = (a_x î + a_y ĵ + a_z k̂)
• Also, b→ = (b_x î + b_y ĵ + b_z k̂)
• A determinant should be created in the following way −

• Please watch the video to understand how to solve a determinant step-by-step.
• After knowing the method, one can get the cross product value instantly as −
• P→ = (a_yb_z - a_zb_y) î - (a_xb_z - a_zb_x) ĵ + (a_xb_y - a_yb_x) k̂

Vectors - Determinant Method Cross Product

Cross Product – Determinant Method

• As a student, you will study about determinants in detail in Mathematics.
• For now, let’s try and understand basic approach of solving a determinant and its usefulness in calculating cross product with speed.
• Determinant method is only applicable when the two vectors are in their resolved form.
• Therefore, let’s say, a→ = (a_x î + a_y ĵ + a_z k̂)
• Also, b→ = (b_x î + b_y ĵ + b_z k̂)
• A determinant should be created in the following way −

This should be solved step by step as shown below −

• First step

This should be expanded as −

î(a_yb_z - a_zb_y)

• Second step

This should be expanded as −

- ĵ(a_xb_z - a_zb_x)

• Third step

k̂(a_xb_y - a_yb_x)

• All the terms should be added. Hence, the cross-product value is −

P→ = (a_yb_z - a_zb_y) î - (a_xb_z - a_zb_x) ĵ + (a_xb_y - a_yb_x) k̂

Calculus -Differentiation

Differential Calculus

• Calculus is a branch of Mathematics and a vast domain in itself. You will study calculus in detail in 12^th standard Mathematics.
• Calculus has extensive use in Physics in all of its domains.
• Differential Calculus is majorly used as a rate measurement tool.

Case Study – Car moving on a straight road

Constant Speed motion

• Let’s say a car is moving on a straight road at constant speed.
• The Distance vs Time plot for the same would look like follows −

• Car is covering equal distances in equal time because it is going at a constant speed.
• Therefore, one can say,
  (y₁ - 0)(x₁ - 0) = (y₂ - y₁)(x₂ - x₁) = (y₃ - y₂)(x₃ - x₂) = (y₄ - y₃)(x₄ - x₃) = Constant
• Rate of change of distance with respect to time is always same.

Increasing/Non-constant Speed motion

• The same car starts to increase its speed of motion.
• Now, let’s say, the Distance vs Time plot would look like follows −

• Car is DOES NOT cover equal distances in equal time because its speed is increasing. In fact, the car covers the larger distances every unit time.
• Therefore, one can say,
  (y₁ - 0)(x₁ - 0) ≠ (y₂ - y₁)(x₂ - x₁) ≠ (y₃ - y₂)(x₃ - x₂) ≠ (y₄ - y₃)(x₄ - x₃)
• Rate of change of distance with respect to time is never same.

Mathematical Analysis of Rate of Change

• Consider any two arbitrary points (x₁,y₁) and (x₂,y₂) on the plot.

• Between points (x₁,y₁) and (x₂,y₂), the rate of change can be defined as −
  Average Rate of Change = (y₂ - y₁)(x₂ - x₁) = ΔyΔx
• The result of this average rate of change can be taken as the average speed of the car.
• However, the plot of the motion is not really a straight line but, a curve.
• Therefore, we are also interested in the value of speed (rate of change of distance w.r.t. time) at every instant (of time) and, not just the average.
• We define instantaneous speed of the car at x = x₀ as follows −

• To physically visualize this, imagine that we start bringing our reference points (x₁,y₁) and (x₂,y₂) closer to each other on the curve towards (x₀,y₀).
• When they are very, very close to (x₀,y₀), the value of both Δx and Δy are very, very close to zero.
• The three points are so close that they are almost on a straight line now and there is no curvature left.

• At this point, the rate of change can be defined as −
  Rate of Change = lim(x₂ - x₁)→0 (y₂ - y₁)(x₂ - x₁) = limΔx→0 ΔyΔx = dydx
• ‘dy’ and ‘dx’ represent infinitesimally small change in ‘y’ and ‘x’ respectively.
• This rate of change obtained can also be called the instantaneous rate of change or, instantaneous speed of the car in the case study.
• Therefore,
  Instantaneous rate of Change = limΔx→0 ΔyΔx = (dydx)_{x = x0}

Relating these results to the moving car case study,

Average Speed of the car between time x₁ and x₂ = (y₂ - y₁)(x₂ - x₁) = ΔyΔx

Instantaneous speed of the car at x₀ = limΔx→0 ΔyΔx = (dydx)_{x = x0}

(dy/dx)as the slope of the tangent

• dydx can also be understood as the slope of the tangent to the curve at x = x₀.
• This is so because dydx is nothing but extremely small value of (y₂ - y₁) divided by extremely small value of (x₂ - x₁).
• Slope of the tangent is defined as: slope = tan θ, where ‘θ’ is the angle tangent makes with the positive x − axis.
• You will learn more about slope in Straight Lines chapter of Mathematics.

(dy/dx) of some common functions

• If y = c where c ∈ constant, then dydx = dcdx = 0
• If y = xⁿ, then dydx = ddx (xⁿ) = n x^(n-1)
• If y = e^x, where "e" is euler′s constant, then dydx = ddx (e^x) = e^x
• If y = a^x, where a ∈ constant, then dydx = ddx (a^x) = a^x ln(a)
• If y = log_ex = ln x, where "e" is euler′s constant, then dydx = ddx (ln x) = 1x
• If y = log_a x, where a ∈ constant, then dydx = ddx (log_ax) = 1x ln a
• If y = sinx, then dydx = ddx (sin x) = cos x
• If y = cos x, then dydx = ddx (cos x) = - sin x
• If y = tan x, then dydx = ddx (tanx) = sec²x
• If y = cosec x, then dydx = ddx (cosec x) = - cosec x cot x
• If y = sec x, then dydx = ddx (sec x) = sec x tan x
• If y = cot x, then dydx = ddx (cot x) = - cosec²x

Addition, Subtraction, Multiplication, Division Rules

• d(u ± v)dx = dudx ± dvdx
• d(u x v)dx = u dvdx + v dudx
• d(u/v)dx = v dudx - u dvdxv²

How to use the formulae - Example

Differentiate: y = sin x + x³ ln x + e^x tan x

• dydx = d(sin x)dx + d(x³ ln x)dx + d(e^x tan x)dx
• dydx = cos x + (ln xd(x³)dx + x³ d(ln x)dx) + (tan xd(e^x)dx + e^x d(tan x)dx)
• dydx cos x + (ln x (3x²) + (x³)1x) + (tan x(e^x) + e^x(sec²x))
• dydx = cos x + (3x² ln x + x²) + (e^xtan x + e^x sec²x)

Chain Rule

Let’s say, y = f(t) and x = g(t).

• Both the variables are functions of ‘t’.
• If we have to calculate dydx, then following method is used −
  dydx = dydt x dtdx
• This can also be written as −
  dydx = dydt x 1dx/dt
• Values of dydt and dxdt can be calculated using the formulae mentioned previously.

Chain Rule - Example

Lets say, y = sin t and x = cos t.

• Then dydx −
  dydx = d(sin t)dt x dtd(cos t)

This can also be written as −

dydx = d(sin t)dt x (1d(cos t)/dt)

dydx = cos t x (1- sin t)

dydx = - (cos tsin t) = - cot(t) = - cot(cos^-1x) = - cot(sin^-1y)

Calculus - Integration

Integral Calculus

Calculus is a branch of Mathematics and a vast domain in itself. You will study calculus in detail in 12^th standard Mathematics.

Calculus has extensive use in Physics in all of its domains.

Integral calculus is majorly used −

• As a reverse process of differentiation
• For calculating area under the curve/graph of any function.

Indefinite Integration

Indefinite Integration can be understood as the reverse process of differentiation.

• For any function y = F(x);
  • If, dydx = f(x),
  • Then ∫ f(x) . dx = F(x) + c [c ∈ constant of integration]

• The symbol ‘∫’ represents the operation of integration.
• The ′c′ value allows us to obtain a family of curves which have the same derivative. Let’s understand the statement −
  • Derivative of any constant number is 0(Zero).
  • Therefore, ddx(F(x) + c) = ddx (F(x)) + ddx (c) = f(x) + 0 = f(x)
  • Therefore, logically, ∫ f(x) . dx = F(x) + c and NOT F(x).
  • Family of curves look like following: (c = 1,2,3,4,etc.,)
    
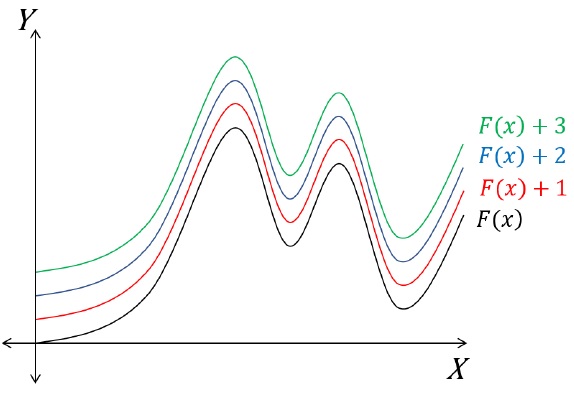
  • Derivative of each curve shown here is f(x).

Example

Let’s say y = tan x;

• Then, dydx = sec²x;
• Therefore
  ∫ sec²x . dx = (tan x) + c [c ∈ constant of integration]

Indefinite Integration – Formulae

• ∫ a . dx = ax + c, where a, c ∈ constant
• ∫ xⁿ . dx = xⁿ⁺¹n+1 + c, where n, c ∈ constant
• ∫ e^x . dx = e^x + c, where e is euler′s constant, c ∈ constant
• ∫ a^x . dx = a^xln a + c, where a, c ∈ constant
• ∫ 1x . dx = ln x + c = log_ex + c, where e is euler′s constant
• ∫ 1x ln a . dx = log_ax + c, where a, c ∈ constant
• ∫ sin x . dx = - cos x + c, where c ∈ constant
• ∫ cos x. dx = - sin x + c, where c ∈ constant
• ∫ sec²x . dx = tan x + c, where c ∈ constant
• ∫ - cosec x cot x . dx = cosec x + c, where c ∈ constant
• ∫ sec x tan x . dx = sec x + c, where c ∈ constant
• ∫ - cosec²x . dx = cot x + c, where c ∈ constant

Addition and Subtraction Rules

Let’s say, u = f(x) and v = g(x).

• ∫ (u ± v) . dx = ∫ u . dx ± ∫ v . dx
• There is no direct multiplication or division rule, unlike differentiation.

Example

Integrate: y = sin x + x³ + e^x

• ∫ y . dx = ∫ (sin x + x³ + e^x) . dx
• This implies, ∫ y . dx = ∫ sin x dx + ∫ x³ . dx + ∫ e^x . dx
• This implies, ∫ y . dx = - cos x + x⁴4 + e^x + c

Definite Integration

Definite Integration could be used to calculate the area under any curve. It could be understood as a limit of the sum. Consider the following curve y = f(x). Our goal is to find the area under the curve between x = 0 and x = x₀.

No.1 plot shows the function y = f(x).

No.2 plot shows an attempt to approximate the area under the curve by using rectangular bars.

• Let’s say the width of each bar is Δx₂.
• Total n₂ such bars are needed to cover the area.
• Approximate area under the curve: n=n₂∑n=0 yΔx₂

No.3 plot is more accurate approximation of area with respect to No.2.

• Let’s say the width of each bar is Δx₃.
• Total n₃ such bars are needed to cover the area.
• Approximate area under the curve: n=n₃∑n=0 yΔx₃

If one decreases the width of each bar (thereby increasing the number of bars required), they will reach to a point when the area defined by the bars is almost accurate.

In that limiting situation (when the area obtained is accurate),

• The width of each bar will be very small (almost zero), hence Δx → 0
• The number of bars required will be very large (almost infinity), hence n → ∞.

Therefore,

limn→∞, Δx→0 n=n∑n=0 yΔx = x₀∫0 y . dx (Δx changes into dx)

Definite integrals have upper and lower limits present on them. As one can see in the above equation, the lower limit is 0(zero) and the upper limit is x₀.

Definite Integration – General Form

For a function, y = f(x), definite integral is defined as −

Here,

• ′a′ is the lower limit and ′b′ is the upper limit of integral.
• F(x) is the function obtained as the result of integration.
• The result also indicates the area under of the curve of y = f(x), between x = a and x = b.

All the formulae of indefinite integration is applicable to definite integration as well.

Definite Integration – Example

For a function, y = x², find 4∫2 y . dx

• 
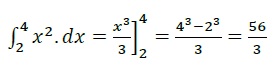
• This also represents area under the curve of y = x² between x = 2 and x = 4.

Problem 1 on Vectors

Problem

A vector a→ makes an angle of 20^o and b→ makes an angle of 110^o with the X-axis. The magnitudes of these vectors are 3 m and 4 m respectively. Find the resultant.

Solution

Now, taking the vectors separately and adding them using Parallelogram Law −

Now, using the formulae for magnitude and direction of the resultant −

|R→| = √|a→|² + |b→|² + 2|a→||b→| cos90^o = 5m

tan α = |b→| sinθ|a→| + |b→| cosθ = 4sin 90^o3 + 4cos 90^o = 43 ⇒ α = tan^-143

The resultant, R→, makes an angle of (α + 20^o) with the X − axis.

Problem 2 on Vectors

Problem

Establish the following vector inequalities geometrically or otherwise −

1. |a→ + b→| ≤ |a→| + |b→|

2. |a→ + b→| ≥ |a→| - |b→|

Solution

For ease of notation, |a→| will be represented by ‘a’ and |b→| will be represented by ‘b’.

Part 1 – Analytical Method

• a→ and b→ are two arbitary vectors.
• The angle between them is θ, it can be acute or obtuse.

Now, we know,

|a→ + b→| = √a² + b² + 2ab cosθ

Max. value of cosθ = 1. (when θ = 0^o or 0 rad)

• Hence, |a→ + b→| ≤ √a² + b² + 2ab
• Or, |a→ + b→| ≤ √(a + b)²
• Or, |a→ + b→| ≤ (|a→| + |b→|) ..... Proved

|a→ + b→| = (|a→| + |b→|) only when cosθ = 1, else it is always, |a→ + b→| < (|a→| + |b→|)

NOTE − a and |a→| are used interchangeably. Same for b and |b→|.

Part 1 – Geometrical Method

• a→ and b→ are two arbitary vectors.
• The angle between them is θ, it can be acute or obtuse.

• Taking S→ = a→ + b→, case by case each time changing the value of angle θ.

• Clearly, |a→ + b→| is maximum when the angle θ = 0 rad. Hence,

|a→ + b→| ≤ |a→| + |b→|

Part 2 – Analytical Method

• a→ and b→ are two arbitary vectors.
• The angle between them is θ, it can be acute or obtuse.

Now, we know,

|a→ + b→| = √a² + b² + 2ab cosθ

Max. value of cosθ = 1. (when θ = 0^o or 0 rad)

• Hence, |a→ + b→| ≤ √a² + b² + 2ab
• Or, |a→ + b→| ≤ √(a + b)²
• Or, |a→ + b→| ≤ (|a→| + |b→|) ..... Proved

|a→ + b→| = (|a→| + |b→|) only when cosθ = 1, else it is always, |a→ + b→| < (|a→| + |b→|)

NOTE − a and |a→| are used interchangeably. Same for b and |b→|.

Part 2 – Geometrical Method

• a→ and b→ are two arbitary vectors.
• The angle between them is θ, it can be acute or obtuse.

• Taking S→ = a→ + b→, case by case each time changing the value of angle θ.

• Clearly, |a→ + b→| is maximum when the angle θ = π2 rad. Hence,

|a→ + b→| ≤ |a→| + |b→|

Problem 3 on Vectors

Problem

î and ĵ are unit vectors along x and y axis respectively.

1. What is the magnitude and direction of î + ĵ , and î − ĵ ?

2. What are the components of a vector A→ = 2î + 3ĵ along the directions of î + ĵ and î − ĵ ?

Solution

Part 1

To calculate î + ĵ , add unit vectors, î and ĵ , using Parallelogram Law.

|R→| = |î + ĵ| = √1² + 1² + 2 × 1 × 1 cosπ2 = √2

tan α = 1 sinπ21 + 1 cosπ2 = 1

α = tan^-11 = π4

To calculate î - ĵ , add unit vectors, î and -ĵ , using Parallelogram Law.

|R→| = |î - ĵ| = √1² + 1² + 2 × 1 × 1 cos(-π2) = √2

tan α = 1 sin(-π2)1 + 1 cos(-π2) = -1

α = tan^-1-1 = -π4

Part 2

We have to calculate components of A→ = 2î + 3ĵ , along (î + ĵ) and (î − ĵ).

Method −

• Extend the (î + ĵ) and (î − ĵ) vectors [obtained from the last part] along their directions to create new X and Y-axis respectively. (As shown in the figure below)
• Draw perpendiculars from arrow head onto the new X and Y axes as shown in the figure. (We follow the same process of resolution as we normally do, only with one change of choosing new directions as X and Y)
• Calculate the magnitude of A→ and the angle between A→ and the new X-axis.
  |A→| = √2² + 3² = √13
  Angle = tan^-11.5 - (π4)
• Write the magnitude of components along each axis.

Magnitude of component along (î + ĵ) [the new + X axis] = √13 cos[tan^-11.5 - (π4)] = 3.53

Magnitude of component along (î - ĵ) [the new - Y axis] = √13 sin[tan^-11.5 - (π4)] = -0.707

Problem 4 on Vectors

Problem

Consider following vectors −

a→ = 3î - 4ĵ + 5k̂

b→ = -2î + ĵ - 3k̂

1. Find the dot product, P = a→ . b→

1. Find the cross product, P = a→ × b→

• By standard method
• By determinant method

Solution

Part 1

P = a→ . b→

P = (3î - 4ĵ + 5k̂) . (-2î + ĵ - 3k̂)

Now, we know,

î . î = ĵ . ĵ = k̂ . k̂ = 1

î . ĵ = ĵ . k̂ = k̂ . î = ĵ . î = k̂ . ĵ = î . k̂ = 0

Hence,

P = -6 - 4 - 15

P = -25 .... Answer

Part 2 - Standard Method

P→ = a→ . b→

P→ = (3î - 4ĵ + 5k̂) × (-2î + ĵ - 3k̂)

Now, we know,

î × î = ĵ × ĵ = k̂ × k̂ = 0

î × ĵ = k̂ ; ĵ × k̂ = î ; k̂ × î = ĵ

ĵ × î = -k̂ ; k̂ × ĵ = -î ; î × k̂ = -ĵ

Hence,

P→ = 3k̂ + 9ĵ - 8k̂ + 12î - 10ĵ - 5î

P→ = 7î - ĵ - 5k̂ .... Answer

Part 2 - Determinant Method

P→ = a→ . b→

P→ = (3î - 4ĵ + 5k̂) × (-2î + ĵ - 3k̂)

Creating the determinant,

P→ = î [(-4)(-3) - (5)(1)] - ĵ [(3)(-3) - (-2)(5)] + k̂ [(3)(1) - (-2)(-4)]

P→ = 7î - ĵ - 5k̂ ... Answer

Problem 5 on Vectors

Problem

Show that the area of the triangle contained between the vectors a→ and b→ is one half of the magnitude of a→ × b→.

Solution

Visualizing the triangle created by the vectors a→and b→,

Shaded region is the area enclosed by the triangle.

• In ΔABC,
  • AC = |b→|
  • AB = |a→|
• Construct the altitude, CD, in the triangle.
• sinθ = CDAC
• CD = AC sinθ = |b→| sin θ

Area = 12 × base × altitude

Area = 12 × AB × CD

Area = 12 × |a→| × |b→| sinθ

Also,

|a→ × b→| = |a→| × |b→| × sinθ

Hence,

Area = 12 |a→ × b→|

Problem 6 on Vectors

Problem

Show that a→.(b→ × c→) is equal in magnitude to the volume of the parallelepiped formed on the three vectors, a→, b→ and c→.

Solution

Visualizing the resulting parallelepiped −

• The base is shaded with brown for better contrast.
• a→ makes an angle of 𝛼 with the Vertical axis. (which can be either X, Y or Z axis depending on the orientation of the parallelepiped)
• Angle between b→ and c→ is ‘θ’.

Now, Volume of Parallelepiped is defined as −

Volume = base × (horizontal height) × (vertical height)

Horizontal height

In the right-angled triangle, it is clear that,

horizontal height = |b→| sinθ

Vertical height

In the right-angled triangle, it is clear that −

vertical height = |a→| cosα

Now,

Volume = base × (horizontal height) × (vertical height)

Hence,

Volume = |a→||b→||c→| sinθ cosα

Calculating, a→ . (b→ × c→) −

a→ . (b→ × c→) = a→ . (|b→||c→| sinθ) n̂

n̂ has the same direction as Vertical-Axis because original a→ and b→ are in the X-Y plane. Hence, angle between a→ and n̂ is α.

(|b→||c→| sinθ) a→ . n̂ = (|b→||c→| sinθ) |a→| cosα

Hence,

a→ . (b→ × c→) = |a→||b→||c→| sinθ cosα

Hence,

Volume = a→ . (b→ × c→)

Problem 1 Differential Calculus

Problem

Calculate the derivatives of following functions −

f(x) = e^x sin x ln x

Solution

To Calculate ddx(f(x)),

Applying product law, d(u x v)dx = u dvdx + v dudx, (consdering u = (sin x ln x), and v = e^x)

ddx(e^x sin x ln x) = (sin x ln x)d(e^x)dx + (e^x) d(sin x ln x)dx

Again, applying product law in the second bracket, (consdering u = ln x, and v = sin x)

(sin x ln x) d(e^x)dx + (e^x) [(ln x) d(sin x)dx + (sin x) d(ln x)dx]

ddx(f((x)) = e^x sin x ln x + e^x ln x cos x + e^x sin xx

Problem 2 Differential Calculus

Problem

Calculate the derivatives of following functions −

f(x) = sin(cos x)

Solution

f(x) = sin(cos x), Calculate ddx(f(x)).

Let’s say t = cos x.

Hence, f(x) = sin(cos x) can be written as, f(t) = sin(t)

Hence,

ddx(f(x)) = d(f(t))dt × dtdx = d(sin(t))dt × dtdx

Differentiating, and putting t = cos x −

cos(cos x) × d(cos x)dx

Hence,

ddx(f(x)) = -sin x cos(cos x)