Motion in Straight Line

Motion pervades the entire universe. Movement of objects happen in many ways like translation, rotation, revolution, etc. In this topic, we develop the basic concepts of motion like position, velocity and acceleration by confining ourselves to rectiliear (or straight line) translational motion. We will extesively use mathematical concepts of vectors and calculus and hence, these become the prerequisites for this topic. Hope you enjoy the chapter.

Motion in 1-D Fundamentals - Kinematics

Kinematics is the study of all causes of motion without diving into the causes of the same.

Study of motion is called Dynamics.

Kinematics vs Dynamics

Following are studied in detail in Kinematics −

• Displacement
• Distance
• Speed
• Acceleration
• Velocity
• Time, etc.

Following are studied in detail in Dynamics −

• Mass
• Torque
• Momentum
• Force
• Angular Momentum
• Gravitation, etc.

1-D (One Dimensional) Kinematics

Motion of particles happen only along a line in one dimension.

In case of straight line like above, motion can happen either along left or right direction.

Sign Convention

• Any one direction (in this case either Left or Right) is arbitrarily chosen to be positive (+).
• The other direction automatically becomes negative (−).

By standards, we can choose mathematically defined positive axis (rightwards direction) as positive direction

Position, Path Length & Displacement

Vectors in 1-D (One dimension)

Straight Line represents one dimension.

Only two directions are possible in one dimension.

Any direction can be chosen to be positive. By convention, the opposite becomes negative.

By Mathematical standards

• Right direction may be represented by positive sign.
• Left direction may represented by negative sign.

Position

Position can be understood as the location of an object with respect to a reference point. It is expressed as a position vector.

Shown below is the position of a cyclist with respect to a lamp post. Cyclist starts at the lamp post and goes to Position 1, 2, 3 and 4 respectively.

Position 1, P1→ = +3 units

Position 2, P2→ = +5 units

Position 3, P3→ = -2units

Position 4, P4→ = -6units

Path Length/Distance

The total length of the path covered by the moving object. It is a scalar.

Following shows the distance covered by the same cyclist.

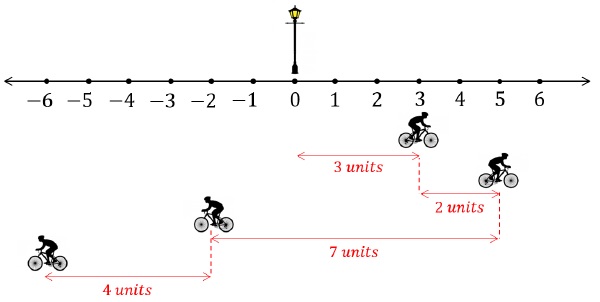
Path Length = 16 units = Distance

Displacement

Shortest distance between the initial and final positions. It is a vector.

Final Displacement, D→ = -6 units

It is interesting to observe the that final displacement vector is same as the final position vector. This is because,

P1→ + P2→ + P3→ + P4→

D→ = 3 + 2 - 7 - 4 = -6 units

General Formula of Displacement

Displacement between two positions starting at P_A→ and ending at P_B→ is defined as −

Displacement, D→ = P_B→ - P_A→

For Example, in the figure below,

Displacement between position 2 and position 4,

D→ = P₄→ - P₂→ = -6 - (+5) = -11 units

Distance and Displacement Relationship

Magnitude of Displacement may or may not be equal to Distance.

For example, in the figure below,

Between P1→ and P2→ −

Distance = 2 units

Magnitude of displacement = |+5 - (+3)| = 2 units

Between P1→ and P3→ −

Distance = 9 units

Magnitude of displacement = |-2 - (+3)| = 5 units

Important Note

• If the object doesn’t change direction during motion, distance is equal to magnitude of displacement. (as evident between P1→ and P2→)
• If the object changes direction during motion, distance is always greater than displacement. (as evident between P1→and P3→)

• Motion in 1-D Fundamentals - Speed

• The Concept

  Rate of change of distance w.r.t. to time is called Speed.

  Average Speed = Total distance coveredTotal time taken = ΔxΔt

  Where,

  ‘Δx’ is the distance/path length

  ‘Δt’ is the time taken

  Instantaneous Speed = limΔ t→0 ΔxΔt = dxdt

  • Speed is a scalar quantity. (Both Distance and Time are Scalars)
  • Speed is always positive. (Distance and Time are never negative)

  Example Problem

  A car drives from Mumbai to Pune, 150 km. It makes several stops in the middle and reaches the destination in 3 hours. Comment on the Average and Instantaneous speed of the car.

  Solution

  For average speed, one can calculate the ratio of total distance and total time.

  Average Speed = ΔxΔt = 150 km3h = 50 km/h

  As the person moves with variable speed and stops frequently, it is impossible to determine instantaneous speed simply by the information provided. Therefore,

  Instantaneous Speed = dxdt = Inderminate

• Motion in 1-D Fundamentals - Velocity

• 
  
• Rate of change of displacement w.r.t. to time is called Velocity.

  • Average Velocity = Total displacementTotal time taken = Δx→Δt
  • Instantaneous Velocity = limΔ t→0 Δx→Δt = dx→dt

  Magnitude of Instantaneous Velocity is equal to Instantaneous Speed.

  • For very small displacement, |displacement→| = distance
  • Hence, |displacement→|time = distancetime

  Velocity is a vector quantity. (Velocity can be either positive or negative.

  Example Problem

  A cyclist moves 20 m towards East from origin O. He then reverses his direction and moves 10 m. Total time taken for the entire motion is 20 s. Comment on the Average Speed and Average Velocity of the cyclist.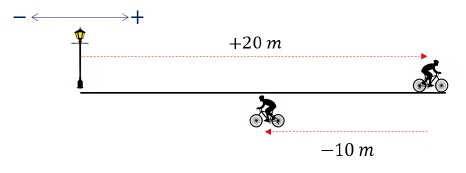

  
  

  Solution

  Total Displacement = 20 - 10 = +10 m

  Total Distance = 20 + 10 = 30 m

  Total time = 20 s

  Therefore,

  Average Speed = Total DistanceTotal time = 3020 = 1.5 m/s

  Average Velocity = Total DisplacementTotal time = 1020 = +0.5 m/s
• 
  

• Motion in 1-D Fundamentals - Acceleration

• Definition

  Rate of change of velocity w.r.t. to time is called Acceleration.

  Average Acceleration = Change in VelocityTotal time = Δv→Δt = v_f - v_it_f - t_i

  Where,

  ‘Δv→’ is the change in velocity,

  ‘Δt’ is the time taken

  Instantaneous Acceleration = limΔ t→0 Δv→Δt = dv→dt

  • Acceleration is a vector quantity. (Velocity is a Vector)
  • Acceleration can be either positive or negative.

  Example Problem

  The Position of an object moving along X - axis is given by −

  x = 4 + 5t² - 2t³

  Calculate the following −

  • Velocity at t = 0s and t = 2s.
  • Acceleration at t = 0s and t = 2s.
  • Average Acceleration between t = 0s and t = 2s

  Solution

  x = 4 + 5t² - 2t³

  Therefore,

  • v = dxdt = 10t - 6t²
  • a = dvdt = 10 - 12t

  Velocity at t = 0s and t = 2s −

  (v)_t=0 = (10t - 6t²)_t=0 = 0 m/s

  (v)_t=2 = (10t - 6t²)_t=2 = -4 m/s

  Acceleration at t = 0s and t = 2s −

  (a)_t=0 = (10 - 12t)_t=0 = 10 m/s²

  (a)_t=2 = (10 - 12t)_t=2 = -12 m/s²

  Average Acceleration between t = 0s and t = 2s −

  Average Acceleration = v_f - v_it_f - t_i = (v)_t=2 - (v)_t=02 - 0

  Average Acceleration = (-12) - (10)2 = -11 m/s²

  Important Points

  When velocity and acceleration have the same direction (or same sign), magnitude of velocity increases. Object speeds up.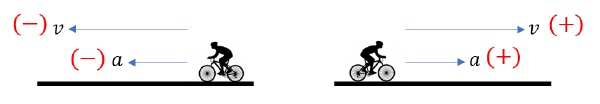

  
  

  When velocity and acceleration have opposite directions (or opposite signs), the magnitude of velocity decreases. Object slows down.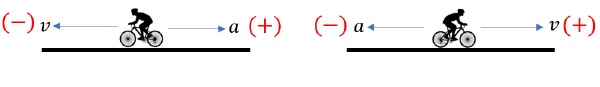

  
  

  This is phenomenon of slowing down is called Retardation. Also, it should never be confused with negative acceleration.

• Position Time Graph

• The Concept

  Position – Time graphs display the motion of a particle by showing the changes of velocity with respect to time.

  For Example,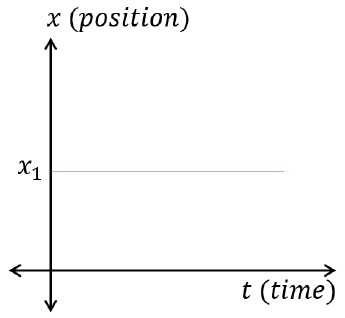

  
  

  Above position – time graph represents an object at rest at position x₁, in positive direction.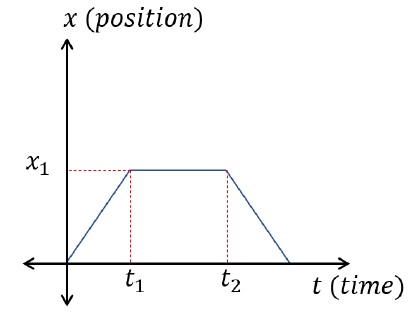

  
  

  Above position – time graph represents particle going at uniform velocity in positive direction until, t = t₁, it stops moving. Finally, it changes direction and starts moving with uniform velocity, v₁, in opposite direction.

  Sailent Points

  Position – Time graphs are also called x − t graphs.

  Slope of Position – Time graph gives instantaneous velocity.

  • Slope of any curve = dydx (Revisit Differential Calculus for more details)
  • Slope of position-time graph = dxdt = inst.velocity

  Also, from previous topic,

  inst speed = magnitude of inst.velocity

  Example Problem 1

  Comment on the motion path taken by the car using the x − t graph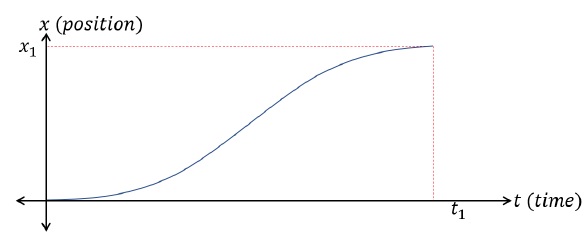

  
  

  Solution

  We know that the slope of x − t graph represents velocity.

  The object starts from rest (because initially the curve is flat, hence slope = 0) at x = 0, and eventually increases speed to a specific value. It stays on that speed for a period of time (constant slope part of the curve) after which it decelerates slowly and comes to rest at position, x = x₁.

  (See video for animation)

  Note − It is important to note that sharp peaks are not possible in any of graphs plotted between kinematic quantities in real life. This essentially means, objects don’t move or come to stop abruptly, rather, they do the same gradually. Hence, the smoothness of graph is always maintained.

  Example Problem 2

  Comment on the motion path taken by the car using the x − t graph.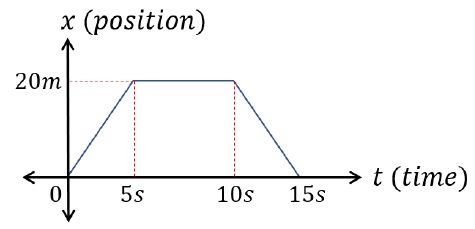

  
  

  Solution

  Velocity in the first 5s, v = dxdt = 20 - 05 - 0 m/s = 4 m/s

  Velocity in between 5s and 10s, v = dxdt = 20 - 2010 - 5 m/s = 0m/s

  Velocity in between 10s and 15s, v = dxdt = 0 - 2015 - 10 m/s = -4 m/s

• Velocity Time Graphs

• 
  

• The Concept

  Velocity – Time graphs display the motion of a particle by showing the changes of velocity with respect to time.

  For Example,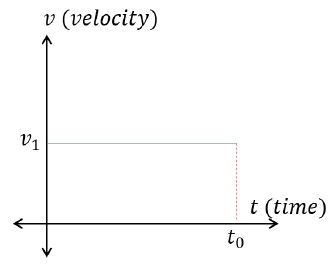

  
  

  Above velocity – time graph represents an object moving with uniform velocity, v₁, in positive direction.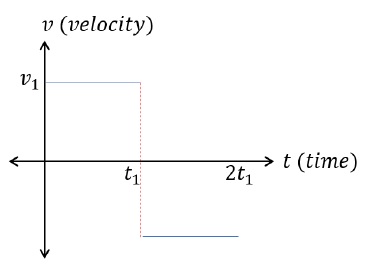

  
  

  Above velocity – time graph represents particle going at uniform velocity in positive direction until, t = t₁, when it changes direction and starts moving with uniform velocity, v₁, in opposite direction.

  Sailent Points

  Velocity – Time graphs are also called v − t graphs.

  Slope of Velocity – Time graph gives instantaneous acceleration.

  • Slope of any curve = dydx (Revisit Differential Calculus for more details)
  • Slope of Velocity - time graph = dxdt = inst.acceleration

  Area under the Velocity – Time graph gives Displacement (or Change in Position).

  • Area under any curve = x₂∫x₁ f(x) . dx
  • Area under Velocity - time graph = t₂∫t₁ v . dt = displacement

  Example Problem 1

  Calculate the acceleration of the object in each interval of time.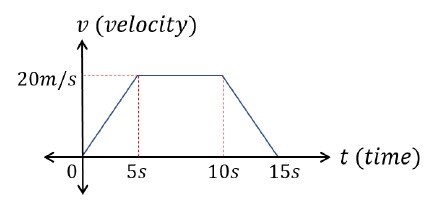

  
  

  Solution

  Velocity in the first 5s, a = dvdt = 20 - 05 - 0 m/s² = 4 m/s²

  Velocity in between 5s and 10s, v = dxdt = 20 - 2010 - 5 m/s² = 0 m/s²

  Velocity in between 10s and 15s, v = dxdt = 0 - 2015 - 10 m/s² = -4 m/s²

  Example Problem 2

  Find the final position of the object if it started at x = 5m.

  
  

  We know area under the curve of v − t graph gives displacement.

  Area = 12 × 20 × 5 + 20 × 5 + 12 × 20 × 5 = 200 m

  Therefore,

  Final Position = Initial Position + Displacement

  Final Position = 5 + 200 = 250 m

  Note −

  • A line parallel to time axis indicates constant velocity motion.
  • Line parallel to velocity axis is not possible. It would indicate particle changing its velocity in no time.
  • 
    

• Acceleration Time Graphs

• The Concept

  Acceleration – Time graphs display the motion of a particle by showing the changes of velocity with respect to time.

  For Example,

  
  

  Above acceleration – time graph represents an object moving with uniform acceleration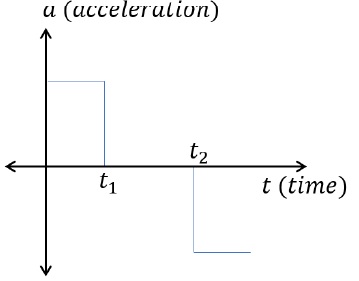

  
  

  Above acceleration – time graph represents particle going at uniform acceleration in positive direction until, t = t₁, when it starts moving with uniform velocity. From t = t₂, the object has negative acceleration and it is velocity starts to retard.

  Salient Points

  Velocity – Time graphs are also called a − t graphs.

  Slope of Velocity – Time graph gives a quantity called Jerk.

  • Slope of any curve = dydx(Revisit Differential Calculus for more details)
  • Slope of acceleration - time graph = dadt = jerk
  • It doesn’t have much applications in Kinematics.

  Area under the Velocity – Time graph gives Change in Velocity.

  • Area under any curve = x₂∫x₁ f(x) . dx
  • Area under acceleration - time graph = t₂∫t₁ a . dt = velocity

  Example Problem 2

  Find the final velocity of the object if it started at v = 5 m/s.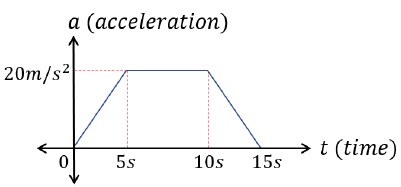

  
  

  We know area under the curve of a − t graph gives velocity.

  Area = 12 × 20 × 5 + 20 × 5 + 12 × 20 × 5 = 200 m/s

  Therefore,

  Final Velocity = Initial Velocity + Change in Velocity

  Final Position = 5 + 200 = 250 m/s

• First Equation of Motion

• The Concept

  Equations of Motion are designed to analyze motions with constant acceleration.

  They relate kinematic variables velocity, displacement, acceleration and time in different ways.

  In daily life, there are many instances of the motion with constant acceleration −

  • Freely falling objects
  • Objects slipping down the incline plane
  • Car starting from rest, etc.

  First Equation of Motion

  v = u + at

  where,

  u = intial velocity,

  v = final velocity

  a = acceleration (must be constant),

  t = time.

  This equation DOES NOT relate to displacement.

  Analytical Proof

  We know that,

  a = dvdt

  Cross multiplying ‘dt’, and integrating both sides,

  dv = a.dt

  v∫u dv = t∫0 a . dt ⇒ v∫u dv = a . t∫0 dt

  v - u = at

  v = u + at

  Graphical Proof

  Following is a v − t graph displaying constant acceleration. (Slope of the curve is constant)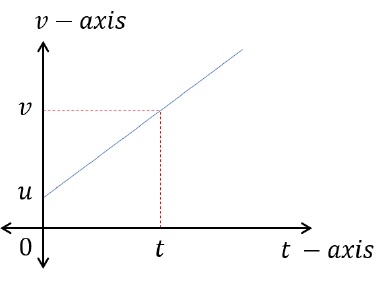

  
  

  • At t = 0 seconds, the particle’s velocity is u m/s.
  • At t = t seconds, the particle’s velocity is v m/s.
  • Slope of this graph gives acceleration.

  a = v - ut - 0 (Acceleration is slope of the v - t graph)

  Rearranging the terms,

  v = u + at

• Second Equation of Motion

• The Concept

  • Equations of Motion are designed to analyze motions with constant acceleration.
  • They relate kinematic variables velocity, displacement, acceleration and time in different ways.
  • In daily life, there are many instances of the motion with constant acceleration
  • Freely falling objects
  • Objects slipping down the incline plane
  • Car starting from rest, etc.

  Second Equation

  S = ut + 12 at²

  Where,

  S = displacement

  u = initial velocity

  a = acceleration (must be constant),

  t = time.

  This equation DOES NOT relate to final velocity.

  Analytical Proof

  We know that,

  v = u + at

  Also,

  v = dSdt

  ‘S’ is the displacement.

  Therefore, equating both,

  dSdt = u + at

  S∫0 dS = t∫0 (u + at) . dt

  S = ut∫0 dt + a t∫0 t . dt

  S = ut + 12 at²

  Graphical Proof

  Following is a v - t graph displaying constant acceleration. (Slope of the curve is constant)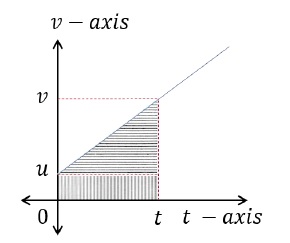

  
  

  At t = 0 seconds, the particle’s velocity is u m/s.

  At t = t seconds, the particle’s velocity is v m/s.

  Area under the curve of v − t graph gives displacement.

  Now,

  S = Area of Rectangle + Area of Triangle

  S = (u - 0) × (t - 0) + 12(v - u)(t - 0)

  S = ut + 12(v - u)(t)

  (Substituting v − u = at, from first equation of motion and rearranging the terms)

  S = ut + 12 at²
• 
  

• Third Equation of Motion

• The Concept

  • Equations of Motion are designed to analyze motions with constant acceleration.
  • They relate kinematic variables velocity, displacement, acceleration and time in different ways.
  • In daily life, there are many instances of the motion with constant acceleration:
  • Freely falling objects
  • Objects slipping down the incline plane
  • Car starting from rest, etc.

  Third Equation

  v² = u² + 2aS

  where,

  v = final velocity,

  S = displacement,

  u = initial velocity,

  a = acceleration (must be constant),

  This equation DOES NOT relate to final velocity.

  Analytical Proof

  We know that,

  a = dvdt

  v = dSdt

  Taking their ratio, we get,

  av = dvdS

  Hence,

  a = vdvdS

  Cross multiplying ‘dS’ and integrating both sides,

  S∫0 a . dS = v∫u v . dv ⇒ aS = v² - u²2

  v² = u² + 2aS

  Graphical Proof

  Following is a v − t graph displaying constant acceleration. (Slope of the curve is constant)

  
  

  At t = 0 seconds, the particle’s velocity is u m/s.

  At t = t seconds, the particle’s velocity is v m/s.

  Area under the curve of v − t graph gives displacement.

  Now,

  S = Area of Rectangle + Area of Triangle

  S = ut + 12(v - u)(t)

  (Substituting t = (v - u)a, from first equation of motion)

  S = u(v - ua) + 12(v - u)(v - ua)

  Rearranging the terms,

  v² = u² + 2aS

• Free Fall Under Gravity

• The Concept

  • All objects are pulled towards the center of the Earth by Gravity.
  • Gravitational acceleration changes as the object moves higher or deeper with respect to surface of the earth. (More details in Gravitation chapter)
  • For all phenomenon happening close to the surface of the earth, we can assume gravitational acceleration to be constant.
  • g = 9.8 m/s² or g = 10 m/s² (approx.)
  • All equations of motion are valid for motion under gravity.

  Redefined equations of motion under gravity

  Table below is drawn assuming the sign convention,

  • Vertically up to be positive (+).
  • Vertically down to be negative(-).

  Equations of Motion - General	Equations of Motion - Under free fall
  v = u + at	v = u - gt
  S = ut + 12 at2	H = ut - 12 gt2
  v2 = u2 + 2aS	v2 = u2 - 2gH

  A student may choose a sign convention of their choice and change the equations of motion under free fall accordingly.

  Visualizing a simple motion under Gravity

  Following case is shown below −

  • A ball is projected upwards with a velocity of 30 m/s.
  • Snapshots of ball’s position and magnitude of velocity are taken every 0.5 seconds.
  • Left set indicates the ball moving upwards and, the Right set indicates it coming downwards. As a student, you should realize that this is only for explanation purposes and in reality, the ball will retrace its path while coming down.
  • Gravitational acceleration, g, is taken to be 10 m/s².

  
  

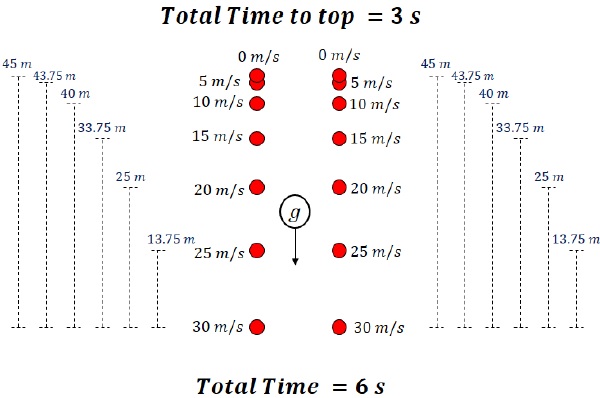
  Salient Points about the motion −

  • Magnitude of velocity changes linearly with time. Every 0.5 second change in time leads to 5 m/s change in velocity. This is because of the first equation of motion,
    v = u + at
    Velocity changes linearly with time.
  • Height (or displacement) changes as a quadratic function of time (See figure). This is because of second equation of motion,
    S = ut + 12 at²
    Displacement changes as a quadratic function of time.
  • Time taken to go up to the maximum height from the point of projection is exactly equal to time taken to come back from maximum height to the point of projection. (In this figure, it’s 3 seconds both ways)

  Many other observations can be made by the student by looking at the diagram carefully which may come in handy while solving problems of motion under gravity or similar phenomenon.

• Relative Velocity

• The Concept

  Relative Velocity could be understood as velocity of one object with respect to the other.

  There are numerous real – life experiences of the same which we can relate to, like −

  • A car overtaking another car.
  • Runners involved in a race, etc.

  Relative Velocity – General Formula

  v→_AB = v→_A - v→_B

  Where, v→_AB = velocity of A with respect to B,

  v→_A = velocity of A with respect to ground,

  v→_B = velocity of B with respect to ground

  E.g. consider two cars, Car A and Car B. Car B is in front of Car A and both are facing East. Now, assuming the sign convention to be,

  • East (Positive)
  • West (Negative)

  Consider the following cases,

  Case 1: Car A and Car B have same velocity with respect to ground

  In this case,

  A ground observer will see both the cars moving East at constant velocity.

  “Car B” driver will see “Car A” in front of him always without any change in separation between them. This is because,

  • v→_AB = v→_A - v→_B
  • Also, v→_A = v→_B, therefore,
  • v→_AB = 0

  Case 2: Car A has larger magnitude of velocity with respect to Car B (same direction of velocity)

  In this case,

  A ground observer will see both the cars moving East and “Car A” overtaking “Car B” at some point of time pertaining to its higher velocity.

  “Car B” driver will see “Car A” approach him. This is because,

  • v→_AB = v→_A - v→_B, Velocity of “Car A” observed by “Car B”.
  • The result of subtraction will be positive.
  • “Car B” will observe “Car A” to be moving in the East direction while approaching him.

  Car A driver will see “Car B” approach him. This is because,

  • v→_AB = v→_B - v→_A, Velocity of “Car A” observed by “Car B”.
  • The result of subtraction will be negative.
  • “Car A” will observe “Car B” to be moving in the West direction while approaching him.

  Case 3: “Car A” has smaller magnitude of velocity with respect to “Car B” (same direction of velocity)

  In this case,

  A ground observer will see both the cars moving East and the separation between them increase more and more as the time passes.

  “Car B” driver will see “Car A” move away from him. This is because,

  • v→_AB = v→_A - v→_B, Velocity of “Car A” observed by “Car B”.
  • The result of subtraction will be negative.
  • “Car B” will observe “Car A” to be moving in the West direction while moving away.

  Car A driver will see “Car B” move away from him. This is because,

  • v→_AB = v→_B - v→_A, Velocity of “Car A” observed by “Car B”.
  • The result of subtraction will be positive.
  • “Car A” will observe “Car B” to be moving in the East direction while moving away.

  Relative Displacement

  Taking the same idea forwards, Relative displacement can be understood as displacement of one object with respect to the other.

  S→_AB = S→_A - S→_B

  where, S→_AB = displacement of A with respect to B,

  S→_A = displacement of A with respect to ground,

  S→_B = displacement of B with respect to ground

  E.g. consider two observers standing at specific positions as shown below,

  
  

  We can say,

  S_A = -4 units,

  Also,

  S_B = 3 units,

  However, displacement of A with respect to B will be,

  S_AB = S_A - S_B = -4 - (+3) = -7 units

  7 units towards the negative direction. (shown in the figure)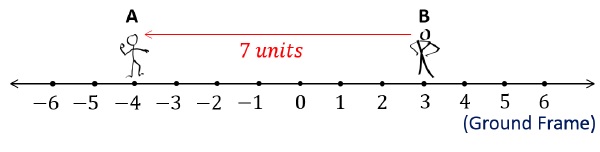

  
  

  Relative Acceleration

  Relative acceleration can be understood as acceleration of one object with respect to the other.

  a→_AB = a→_A - a→_B

  where, a→_AB = displacement of A with respect to B,

  where, a→_A = displacement of A with respect to ground,

  where, a→_B = displacement of B with respect to ground

• Problem 1 on Motion in a Straight Line

• Problem

  A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s.

  • Plot the x − t graph of his motion.
  • Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.

  Solution

  Following is the x − t graph of drunkard’s motion.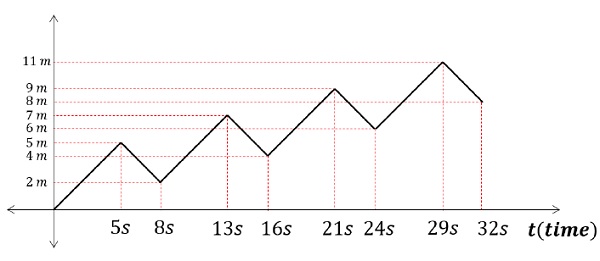

  
  

  Part 2 – Analytical Solution

  Given in the problem,

  • Every 5 s he moves 5 m forward and the next 3 s he moves 3 m backward.
  • To fall in the pit, he has to travel 13 m.

  Note − He can never fall in the pit during the backward movement because while moving back he is simply occupying the positions he already crossed during forward motion.

  Therefore,

  Let the total number of forward steps be ′x′.

  Hence, total number of backward steps, ′(x − 1)′. [See NOTE]

  Therefore,

  5x - 3(x - 1) = 13

  2x = 10

  x = 5

  Hence, he took 5 steps forward and 4 steps backward.

  Total Time = Total Length × (1s) = 5 × 5 + 4 × 3 = 37 s

  Part 2 – Graphical Solution

  Continue drawing the graph till x = 13 m, is crossed.

  We see that this happens at t = 37 s.

  Hence, that is the time taken for him to fall in the pit.

  (Notice how the “NOTE” in the last section can be visualized using the graph below. The result can only lie on the longer line showing the increase in displacement.)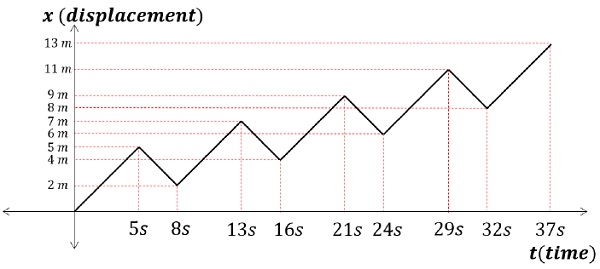

  
• 
  

• Problem 2 on Motion in a Straight Line

• Problem

  Consider the following x − t graph.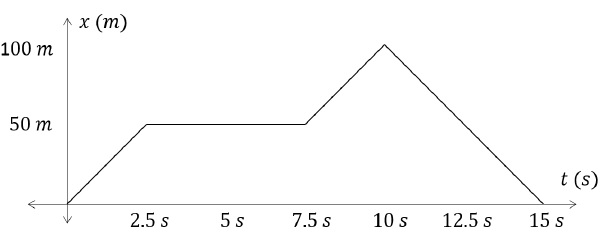

  
  

  Find,

  • The average velocity during 0 s to 10 s.
  • Instantaneous velocity at 2 s, 5 s, 8 s, 12 s.

  Solution

  We know that, average velocity is simply the ratio of total displacement and total time. Therefore,

  Average velocity during 0 s to 10 s is,

  Average Velocity = Total DisplacementTotal Time

  Average Velocity = 10010 = 10 m/s

  Instantaneous Velocity at any point is simply the slope of tangent to the curve at that point. Therefore,

  At t = 2s,

  Slope of Tangent = 50 - 02.5 - 0 = 20 m/s

  At t = 5s,

  Slope of Tangent = 50 - 507.5 - 2.5 = 0 m/s

  At t = 8s,

  Slope of Tangent = 100 - 5010 - 7.5 = 20 m/s

  At t = 12s,

  Slope of Tangent = 0 - 10015 - 10 = -20 m/s

• Problem 3 on Motion in a Straight Line

• Problem

  From the velocity – time graph shown below, find the distance travelled by the particle during first 40 seconds. Also find the average velocity during this period.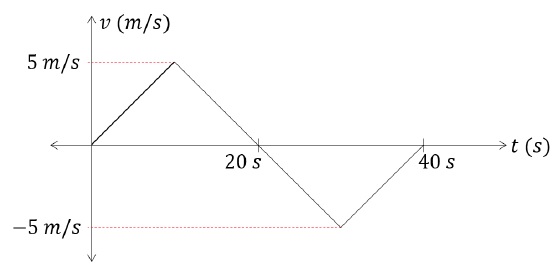

  
  

  Solution

  Let’s analyze the graph first.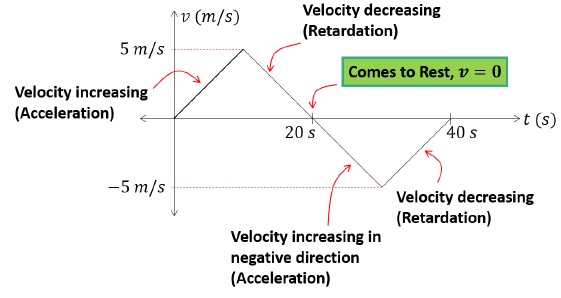

  
  

  For the first segment (t = 0s to t = 10s)

  • Slope of the line is positive.
  • Velocity is increasing w.r.t to time. This indicates acceleration.

  For the second segment (t = 10s to t = 20s)

  • Slope of the line is negative.
  • Velocity is decreasing w.r.t to time. This indicates retardation.

  For the third segment (t = 20s to t = 30s)

  • Slope of the line is negative.
  • Velocity is increasing w.r.t. to time. This indicates acceleration in the opposite direction.
    (IMPORTANT: Negative acceleration is NOT same as retardation)

  For the fourth segment (t = 30s to t = 40s)

  • Slope of the line is positive.
  • Velocity is decreasing w.r.t. to time. This indicates retardation.

  Calculating Distance and Average Velocity

  Area under the curve of a v − t graph gives displacement.

  Therefore,

  Displacement between t = 0 s to t = 20 s,

  Area under the curve = 12 × 5 × 20 = 50 m

  Displacement between t = 20 s to t = 40 s,

  Area under the curve = 12 × (-5) × (40 - 20) = -50 m

  Now, total distance covered is the sum of magnitudes of both the displacements. (Because distance simply indicates the length of the path travelled)

  Total Distance = |50| + |(-50)| = 100 m

  We know that,

  Average Velocity = Total displacementTotal time = 50 - 5040 = 0 m/s

• Problem 4 on Motion in a Straight Line

• Problem

  A person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the position of 3^rd, 4^th and 5^th ball when the 6^th ball is being dropped.

  Solution

  Let’s discuss the motion path of the balls first.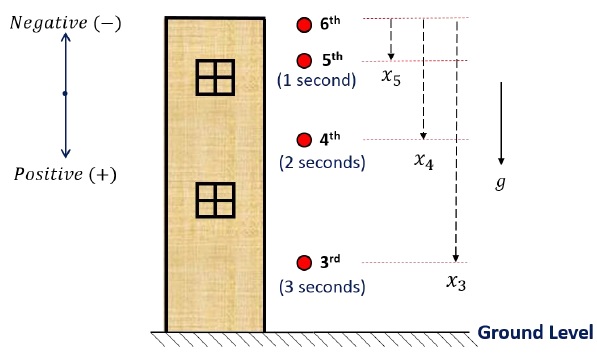

  
  

  Motion path of the balls

  The sign convention chosen for this problem is −

  • Down is positive
  • Up is negative

  All balls start their motion from rest. Hence, initial velocity is zero for all of them. (u = 0)

  Because the person drops a ball every second, it is clear that when the 6th ball is dropped,

  • 3^rd ball has already travelled for 3 seconds.
  • 4^th has already travelled for 2 seconds.
  • 5^th ball has already travelled for 1 second.

  Let the displacement of n^th ball be x_n.

  Calculating position of 3^rd ball

  Initial Velocity of each ball, u = 0 m/s

  Acceleration, g = +10 m/s²

  Time for which 3^rd ball has travelled = 3 s

  Taking roof-top point as the origin, displacement of 3^rd ball, S₃ is,

  S = ut + 12 at²

  S₃ = 0 × (3) + 12(9.8) × (3)²

  S₃ = 44.1 m

  Calculating position of 4^th ball

  Initial Velocity of each ball, u = 0 m/s

  Acceleration, g = +10 m/s²

  Time for which 3^rd ball has travelled = 2 s

  Taking roof-top point as the origin, displacement of 4^th ball, S₄ is,

  S = ut + 12 at²

  S₄ = 0 × (2) + 12(9.8) × (2)²

  S₄ = 19.6 m

  Calculating position of 5^th ball

  Initial Velocity of each ball, u = 0 m/s

  Acceleration, g = +10 m/s²

  Time for which 3^rd ball has travelled = 1 s

  Taking roof-top point as the origin, displacement of 5^th ball, S₅ is,

  S = ut + 12 at²

  S₅ = 0 × (1) + 12(9.8) × (1)²

  S₅ = 4.9 m

• Problem 5 on Motion in a Straight Line

• Problem

  A car moving along a straight highway with speed of 126 km/h is brought to a stop within a distance of 200m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?

  Solution

  This is the case of retardation. Therefore,

  For the sign convention, assuming the direction of motion of the car to be positive,

  Initial velocity of the car, u = 126 km/h = 126 × 10003600 = 35 m/s

  Final velocity of the car, v = 0 m/s (Car comes to rest)

  Displacement of the car, S = 200m

  Acceleration is expected to have a negative sign according to the sign convention chosen above.

  Also. acceleration is given to be uniform, hence the equations of motion could be applied.

  v² = u² + 2aS

  0 = (35)² + 2a(200)

  a = -3.06 m/s²

  S₄ = 19.6 m

  To calculate the time taken, we use,

  v = u + at

  0 = 35 - 3.06 × t

  t = 353.06 = 11.4 s

• Problem 6 on Motion in a Straight Line

• Problem

  A ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground.

  Solution

  Analyzing motion path of the ball,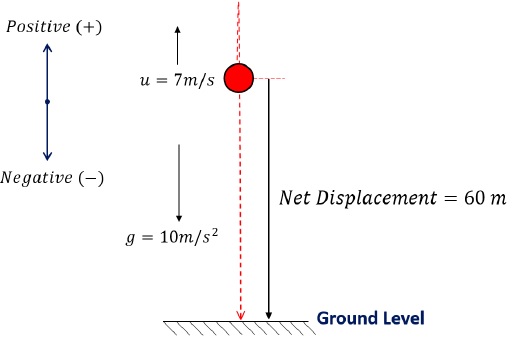

  
  

  When the ball is released from the balloon, it possesses an upward velocity of 7 m/s. Therefore, the ball will move upwards, attain a maximum height and then eventually descend down.

  Assuming sign convention to be −

  • Upwards – Positive
  • Downwards – Negative

  We can say that,

  Initial Velocity, u = 7 m/s

  Acceleration, g = −9.8 m/s²

  Displacement, S = -60 m

  Using, S = ut + 12 at², we get,

  -60 = 7t + 12 (-9.8) t²

  4.9 t² - 7t - 60 = 0

  t = 4.28 s ≈ 4.3 s

• Problem 7 on Motion in a Straight Line

• Problem

  A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one − tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.

  Solution

  Salient points about the problem −

  • Ball’s motion will reverse its direction at every impact.
  • Equations of motion will be applicable because the motion is happening under constant acceleration.
  • We will analyze each impact and subsequent motion after it step-by-step.
  • Sign convention chosen for this is,
    • Up is negative
    • Dowm is positive

  Before First Impact

  
  

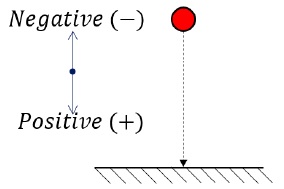
  Ball drops from the height to hit the ground for the first impact.

  Height = 90 m

  Calculating velocity of first impact using, v² = u²+ 2gH, (u = 0; S = 90),

  v₁ = √2gH = 30√2 m/s = 42.42 m/s

  Time elapsed before first impact using, H = ut + 12 gt², (u = 0; H = 90),

  t = 4.24 s

  Between First and Second Impact

  
  

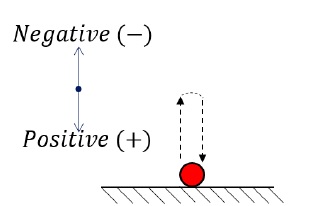
  Problem says, ball loses one − tenth of its speed upon every impact. This implies nine − tenth of the velocity is retained.

  Therefore, magnitude of take-off velocity after first impact,

  u₂ = 910 × v₁ = 910 × 30√2 = 27√2 m/s = 38.18 m/s

  Time taken to reach the highest point using, v = u₂ + at, (v = 0)

  0 = -27√2 + gt

  t = 3.82 s

  Total time before second impact, (Time taken to go up and then come down is simply twice the time taken to go up)

  2 × t = 7.64 s

  Between Second and Third Impact

  
  

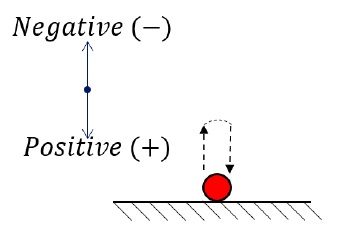
  Problem says, ball loses one − tenth of its speed upon every impact. This implies nine − tenth of the velocity is retained.

  Magnitude of take-off velocity after second impact,

  u₃ = 910 × u₂ = 910 × 27√2 = (24.3)√2 m/s = 34.36 m/s

  Time taken to reach the highest point using, v = u₃ + at, (v = 0)

  0 = -24.3√2 + gt

  t = 3.44 s

  Total time before third impact, (Time taken to go up and then come down is simply twice the time taken to go up)

  2 × t = 6.88 s

  The final Velocity – Time graph

  
  

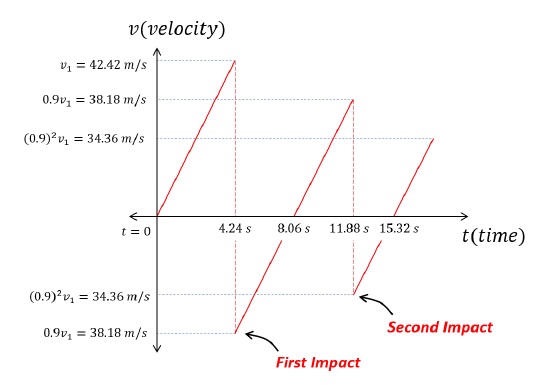
  The final Speed – Time graph

  

• Problem 8 on Motion in a Straight Line

• Problem

  A jet airplane travelling at the speed of 500 km/h ejects its products of combustion at the speed of 1500 km/h relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?

  Solution

  Assume the jet plane is travelling East. Hence, the sign convention we choose is −

  • East as positive direction.
  • West as negative direction.

  Velocity of jet plane with respect to ground, v_J = 500 km/h

  Velocity of exhaust with respect to jet plane, v_EJ = −1500 km/h

  Using the equation of relative velocity,

  v_EJ = v_E - v_J

  -1500 = v_E - (500)

  v_E = -1000 km/h

  Hence, Speed of Exhaust w.r.t. ground = 1000 km/h
• Problem 9 on Motion in a Straight Line

• Problem

  Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km/h in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s². If after 50s, the guard of B just brushes past the driver of A, what was the original distance between them?

  Solution

  First, we will solve the problem as observers in Ground Frame.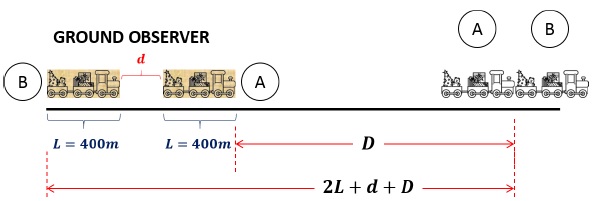

  
  

  Velocity of Train A, v_A = 72 km/h = 20 m/s

  Total time of the event, t = 50s

  Displacement of Driver of A, D = v_A × t = 20 × 50 = 1000 m

  Displacement of Guard of Train B = 2L + d + D = (1800 + d) m

  Acceleration of Train B, a_B = 1 m/s²

  Using, S = ut + 12 at², for Train B, we can write,

  (1800 + d) = 20 × 50 + 12 × 1 × (50)²

  d = 450 m (Separation between two trains)

  Separation between Guard (Train B) and Driver (Train A),

  Separation = 400 + 450 + 400 = 1250 m

  Second, we will solve the problem as observers in the frame of A’s driver.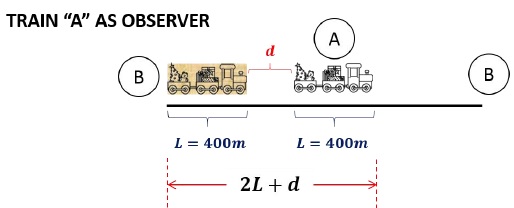

  
  

  Initial velocity of both trains w.r.t. to ground = 72 km/h = 20 m/s

  Initial velocity of Train B w.r.t. to Train A, v_BA = 20 − 20 = 0 m/s

  Total time of the event, t = 50 s

  Displacement of Guard of B w.r.t. Driver of A = 2L + d = (800 + d) m

  Acceleration of Train B w.r.t Train A, a_BA = 1 m/s²

  Using, S_BA = u_BAt + 12a_BA t², in the frame of Train A, we can write,

  (800 + d) = 0 × 50 + 12 × 1 × (50)²

  d = 450 m(Separation between two trains)

  Separation between Guard (Train B) and Driver (Train A),

  Separation = 400 + 450 + 400 = 1250 m

• Problem 10 on Motion in a Straight Line

• Problem

  On a two-lane road, car A is travelling with a speed of 36 km/h. Two cars B and C approach car A in opposite directions with a speed of 54 km/h each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?

  Solution

  Assume Car A to be moving East.

  Therefore, Car B moves East approaching car A from behind.

  Car C moves West approaching car B from front.

  Following sign convention is assumed for this problem −

  
  

  Therefore,

  Velocity of car A = +36 km/h = 10 m/s

  Velocity of car B = +54 km/h = 15 m/s

  Velocity of car C = −54 km/h = −15 m/s

  In the frame of reference of Car A −

  Velocity of B with respect to A, v_BA = v_B − v_A = 15 − (+10) = 5 m/s

  Velocity of C with respect to A, v_CA = v_C − v_A = −15 − (+10) = −25 m/s

  Assume car B moves with an acceleration of a_B, to overtake A.

  Therefore, a_BA = a_B - a_A = a_B - 0 = a_B

  Visualizing the Problem in the Frame of Car A

  
  

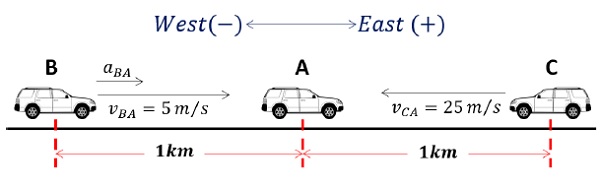
  To avoid the accident, B has to reach A before C does. We will calculate the bare minimum acceleration of Car B so that it reaches A simultaneously with Car C. Any acceleration higher than that will make Car B reach Car A first and hence, avoid the accident.

  Therefore,

  Time taken by C to reach A, t = 100025 = 40 s (Calculated in the Frame of Car A)

  Same time is available for B to overtake A.

  Applying, S = ut + 12 at², (Equation applied in the Frame of Car A)

  1000 = 5 × 40 + 12 × a_B × (40)²

  a_B = 1 m/s²

• Problem 11 on Motion in a Straight Line

• Problem

  Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes.

  A man cycling with a speed of 20 km/h in the direction A to B notices that a bus goes past him every 18 minutes in the direction of his motion, and every 6 minutes in the opposite direction.

  What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?

  Solution

  Assume the cyclist to be moving East.

  Therefore,

  • buses moving East approach cyclist from behind.
  • buses moving West approach cyclist from front.

  Following sign convention is assumed for this problem −

  
  

  Assume that speed (magnitude of velocity) of buses with respect to ground is (v) km/h.

  Velocity of buses moving East is assumed to be v→_E.

  Velocity of buses moving West is assumed to be, v→_W.

  Velocity of cyclist is assumed to be, v→_C.

  Therefore,

  Velocity of buses moving East w.r.t to cyclist,

  v→_EC = (v→_E - v→_C) = (v - 20) km/h

  Velocity of buses moving West w.r.t to cyclist,

  v→_WC = (v→_W - v→_C) = (-v - 20) = -(v + 20) km/h

  Now,

  Because buses leave in either direction every ‘T’ minutes, separation between any two busses in the same direction is,

  Separation = (d) km = vT

  Buses moving East pass the cyclist every 18 minutes. Therefore, with respect to cyclist,

  d(v - 20) = 18 minutes

  Buses moving West pass the cyclist every 6 minutes. Therefore, with respect to cyclist,

  -d-(v + 20) = 6 minutes

  Note: Busses travelling West will have negative displacement due to chosen sign convention. Hence, the negative sign in the numerator of second equation.

  Taking their ratio,

  (v + 20)(v - 20) = 3

  v = 40 km/h

  Now,

  To calculate ‘𝑇’, substituting the value of ‘𝑑’ as ‘𝑣𝑇’ in the first equation, d(v - 20) = 18 minutes,

  vT(v - 20) = 18 minutes

  Putting the value of ‘v’,

  40 × T(40 - 20) = 18 minutes

  2 × T = 18 minutes

  T = 9 minutes

• Problem 12 on Motion in a Straight Line

• Problem

  On a long horizontally moving belt, a child runs to-and-fro with a speed of 9 km/h (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km/h. For an observer on a stationary platform outside, what is the,

  • Speed of the child running in the direction of motion of the belt?
  • Speed of child running opposite to the direction of motion of the belt?
  • Time taken by the child in first two problems?

  Which answers alter if motion is viewed by one of the parents?

  Solution

  Velocity of child with respect to belt is referred to as, v→_CB.

  Velocity of child with respect to ground is referred to as, v→_C.

  Velocity of belt with respect to ground is referred to as, v→_B.

  Now,

  Solving each part of the problem,

  Part 1 – Child running in the direction of belt’s motion

  
  

  Using the concept of relative velocity, (Sign convention taken into account)

  v_CB = v_c - v_B

  9 = v_c - 4

  v_c = 13 km/h

  Part 2 – Child running opposite to direction of belt’s motion

  
  

  Using the concept of relative velocity,

  v_CB = v_C - v_B

  -9 = v_C - 4

  v_C = -5 km/h

  Part 3(a) – Time taken by child in Part 1

  
  

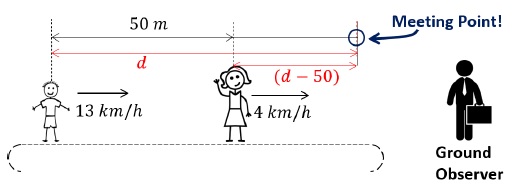
  Above diagram is perceived by the ground frame observer.

  • The parent (mother in this case) will have a velocity of +4 km/h with respect to ground observer because she is standing stationary on the belt, which itself is moving at a velocity of +4 km/h.
  • Velocity of child with respect to ground observer is perceived to be +13 km/h (See Part 1).
  • The meeting point will be somewhere on the right of the of both parent and child as shown in the figure.

  Initial separation between parent and the child = 50 m

  Let the child travel a distance of ‘d’ metres.

  The distance travelled by mother = (d − 50) metres [See figure]

  Time taken to reach the meeting point is, ‘t’. (same for both parent and child)

  Therefore, equation for the parent (mother),

  (d - 50)/1000 = 4 × t

  equation for the child,

  (d/1000) = 13 × t

  Eliminating ‘d’,

  13t = (501000) + 4t

  t = 509 × 1000 = 5.551000h = 19.98 s

  Hence, total time elapsed in this case is, t = 19.98 s

  Part 3(b) – Time taken by child in Part 2

  
  

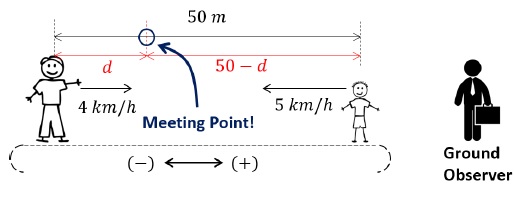
  Above diagram is perceived by the ground frame observer.

  • The parent (father in this case) will have a velocity of +4 km/h with respect to ground observer because he is standing stationary on the belt, which itself is moving at a velocity of +4 km/h.
  • Velocity of child with respect to ground observer is perceived to be −5 km/h (See Part 2).
  • The meeting point will be somewhere on the right of the of the parent and left of the child as shown in the figure.

  Initial separation between parent and the child = 50 m

  Let the parent (father) travel a distance of ‘d’ metres.

  The distance travelled by child = (50 − d) metres [See figure]

  Time taken to reach the meeting point is, ‘t’. (same for both parent and child)

  Therefore, equation for the parent (father),

  d/1000 = 4 × t

  equation for the child,

  (50 - d)/1000 = 5 × t

  Eliminating ‘d’,

  4t = 501000 - 5t

  t = 509 × 1000 = 5.551000h = 19.98 s

  Hence, total time elapsed in this case is also, t = 19.98 s

  When motion of the child is observed with respect to parents

  Parents are at rest with respect to the conveyor belt.

  • Hence, they will perceive the velocity of child as 9 km/h, which is simply his velocity w.r.t. to belt.
  • Total time taken by the child to move between parents won’t change.

  t = Separation of Parents on the beltVelocity of child w.r.t to belt = (50/1000)9 = 5.551000h = 19.98 s